Generalized Linear Models in 3D • regress3d

Introduction

A multiple linear regression creates a flat regression surface. A multiple linear regression with an interaction term can be depicted as a curved regression surface with linear marginal effects. A generalized linear model (glm) takes a linear component as a variable in a nonlinear function, creating a curved regression surface with nonlinear marginal effects. The functionality of add_3d_surface() and add_marginals() in a glm is the same as in a linear regression model. However, the visuals are sufficiently different to merit a separate description.

This article demonstrates a binomial model and a Gamma model.

At this time, regress3d has been tested on binomial models, negative binomials, and Gammas, but it should work for all generalized linear models.
Interaction terms are also allowed in the graphics for generalized linear regressions.
The function add_jitter() is demonstrated in the example of a binomial glm.

Setup

The package regress3d is built on the syntax of plotly in R. Both libraries are called in the initial setup.

library(regress3d)
library(plotly)

Logistic Regression

Data

The variables in the regression are county level measures from 2016. For pedagogical purposes, the variables are chosen to emphasize the s-shape of a logistic regression.

plurality_Trump16: a binary variable indicating whether the plurality of a county voted for Trump in 2016.
any_college: the percent of adults in the county that had ever enrolled in college, regardless of whether they graduated.
prcnt_black: the percent of the county that identified as Black in the 2016 census.

2D plot of a logistic regression

For reference, a two dimensional plot of logistic regression can look like this.

The outcome variable, plurality_Trump16, is binary. We use ggplot2::geom_jitter() to reveal the density of observations for counties that have very few Black residents.
In this case the explanatory variable prcnt_black is continuous.
The logistic regression model requires an s-shape for the predicted probabilities so that they cannot exceed the range $(0,1)$ .

county_data %>%
  ggplot(aes(x = prcnt_black, y = plurality_Trump16)) +
  geom_jitter(width = 0, height = 0.1, alpha = 0.5) + 
  geom_smooth(method = "glm", method.args = list(family = "binomial")) +
  theme_classic()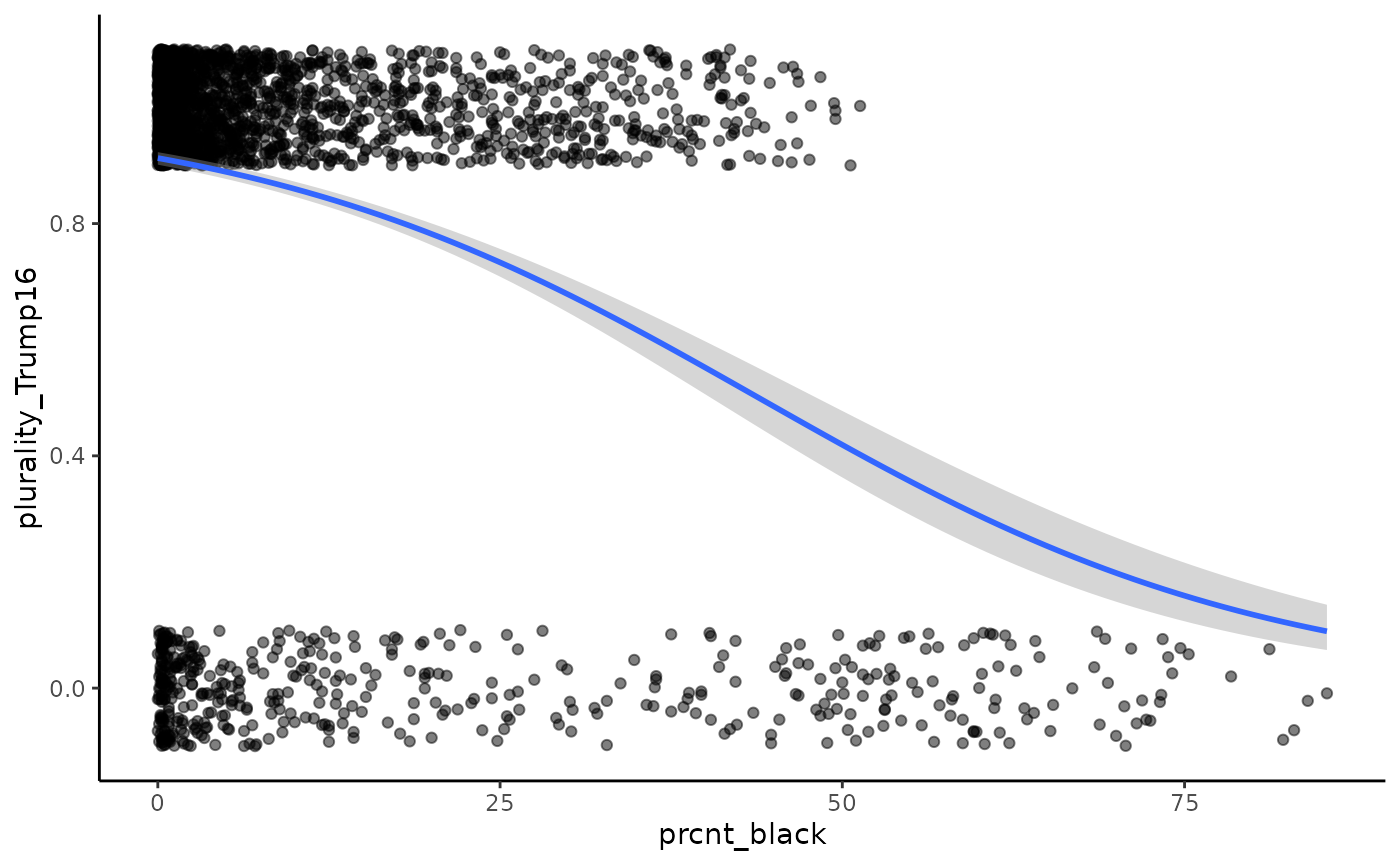

3D plot of a logistic regression

The three dimensional plot adds education, any_college, to the logistic regression depicted above.

mymodel <- glm(plurality_Trump16 ~ any_college+prcnt_black, 
               data = county_data, 
               family = "binomial")

plot_ly( data = county_data,
         x = ~any_college,
         y = ~prcnt_black,
         z = ~plurality_Trump16) %>%
  add_jitter(x_jitter = 0, y_jitter = 0, z_jitter = 0.1,
             size = 1, color = I('black'))%>%
  add_3d_surface(model = mymodel, ci = T) %>%
  add_marginals(model = mymodel, ci = T)

More on marginal effects

In a linear regression, the marginal effect of $x_1$ stays constant for all values of $x_2$ . This is true for generalised linear models as well. However, note that for a given range of $x_1$ , the magnitude of the change in the outcome $y$ can depend on the value of $x_2$ . This is depicted in the image below, where the marginal effects of education ( $x_1$ ) are shown for two different values of % Black ( $x_2$ ).

This is depicted in the image below. Each call to add_marginals() specifies a different constant value for the marginal effect of % Black ( $x_1$ ) using the argument x2_constant_val.

plot_ly( data = county_data,
         x = ~any_college,
         y = ~prcnt_black,
         z = ~plurality_Trump16) %>%
  add_jitter(, x_jitter = 0, y_jitter = 0, z_jitter = 0.1,
             size = 1, color = I('black'))%>%
  add_3d_surface(model = mymodel, ci = T) %>%
  add_marginals(model = mymodel, ci = T, omit_x2=T,
                x1_direction_name = "Marginal effect of education<br>with % Black held constant at its mean 8.75%") %>%
  add_marginals(model = mymodel, ci = T, omit_x2 =T,
                x2_constant_val = 50,
                x1_direction_name = "Marginal effect of education<br>with % Black held constant at 50%")

Click, hold, and drag the regression surface to spin it. See the article on linear models for more information on how to manipulate this graphic.

Numeric regression results

This graphic corresponds to the following numerical regression results.


	plurality of county voted for Trump in 2016

County college experience		-0.119^*
		(0.006)

% Black	-0.054^*	-0.086^*
	(0.003)	(0.004)

Constant	2.348^*	9.228^*
	(0.069)	(0.406)


Observations	3,139	3,139

Note:	* p<0.05

Gamma Model

Data

The variables in the regression are county level measures from 2016.

median_income16: county level median income. This outcome variable is chosen to allow for a Gamma model, as it is positive continuous, and right skewed.
any_college: the percent of adults in the county that had ever enrolled in college, regardless of whether they graduated.
prcnt_black: the percent of the county that identified as Black in the 2016 census.

The regression is weighted by pop_estimate16, the number of people in a county, to capture the influence of large counties.

2D code and graphic

For reference, a two dimensional plot of Gamma regression can look like this.

county_data %>%
  ggplot(aes(x = any_college, y = median_income16)) +
  geom_point() + 
  geom_smooth(method = "glm", method.args = list(family = "Gamma")) +
  theme_classic()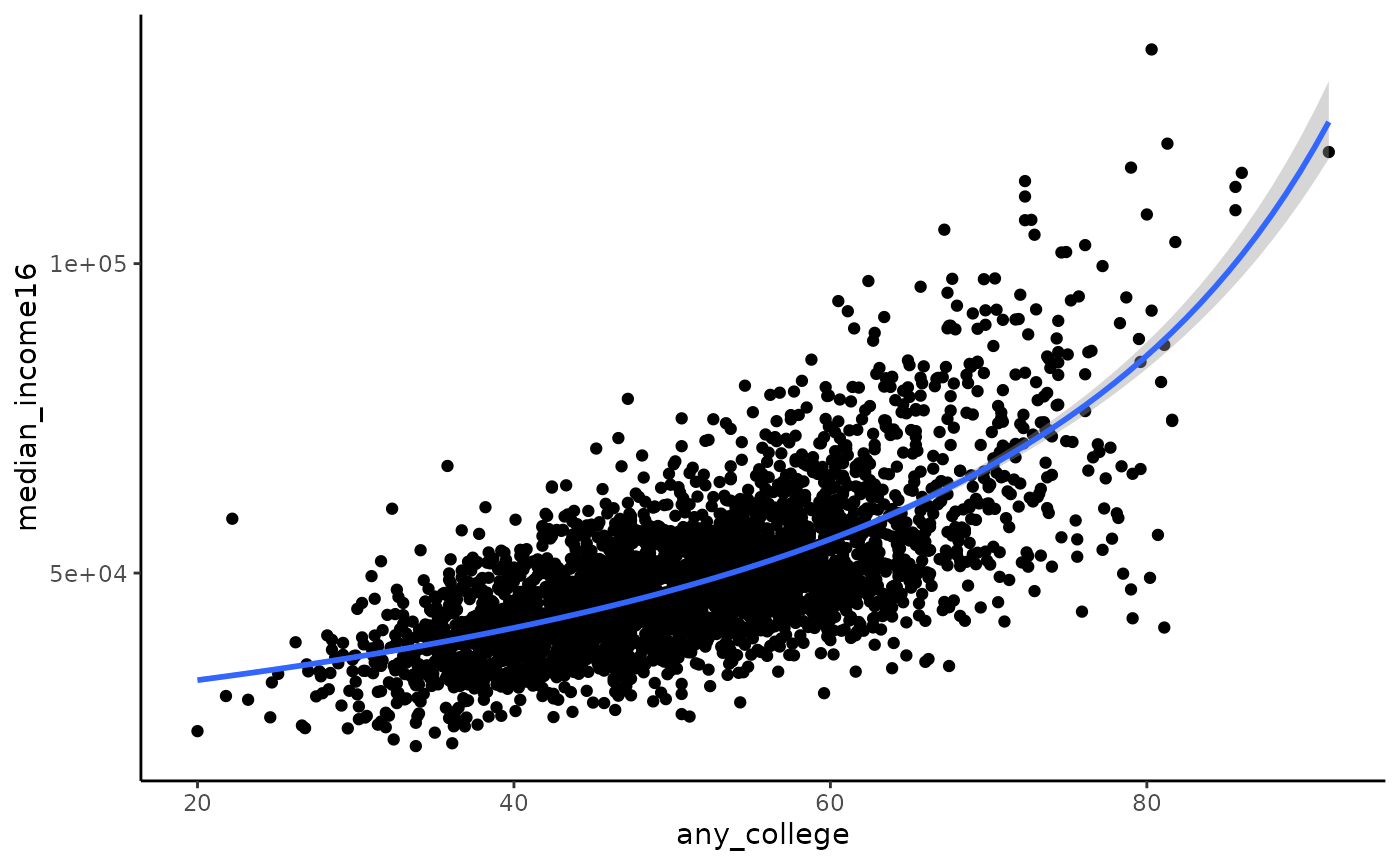

3D code and graphic

The three dimensional plot adds prcnt_black to the Gamma regression depicted above as well as weights for the county population.

The code starts by specifying a model. We then create a plotly::plot_ly() object using the same variables. Next layer on the scattercloud, 3D surface, marginals, and labels. Note that regression notation uses $x_1$ and $x_2$ to represent the explanatory variables, and $y$ for the outcome. The plotly command denotes the explanatory variables as $x$ and $y$ , and the outcome variable is $z$ .

county_data$median_income16_1k <- county_data$median_income16/1000

mymodel <- glm(median_income16_1k ~ prcnt_black +any_college, 
               data = county_data, weight = pop_estimate16, family = Gamma)

plot_ly( data = county_data,
         x = ~prcnt_black,
         y = ~any_college,
         z = ~median_income16_1k) %>%
  add_markers(size = ~pop_estimate16, color = I('black')) %>%
  add_3d_surface(model = mymodel)%>%
  add_marginals(model = mymodel)

Click, hold, and drag the regression surface to spin it. See the article on linear models for more information on how to manipulate this graphic.

More on marginal effects

plot_ly( data = county_data,
         x = ~prcnt_black,
         y = ~any_college,
         z = ~median_income16_1k) %>%
  add_markers(size = ~pop_estimate16, color = I('black')) %>%
  add_3d_surface(model = mymodel, ci = T) %>%
  add_marginals(model = mymodel, ci = T, omit_x2=T,
                x1_direction_name = "Marginal effect of % Black<br>with education held at the mean 51.24%") %>%
  add_marginals(model = mymodel, ci = T, omit_x2 =T,
                x2_constant_val = 80,
                x1_direction_name = "Marginal effect of % Black<br>with education held constant at 80%")